9. Sequences

Exercises

a. Definition of Sequences

In each problem, assume that the pattern continues and write out the general term of the sequence. Assume the terms are numbered beginning with $n=1$.

$\{1,3,5,7,9,\cdots\}$

$a_n=2n-1$

If we add $1$ to this sequence, we get the sequence of even numbers, or $2n$. Since we added $1$, we have to subtract $1$ from that sequence. So the sequence is: \[ a_n=2n-1 \]

ad
$\left\{\dfrac{3}{2},\dfrac{3}{4},\dfrac{3}{8},\dfrac{3}{16},\dfrac{3}{32}\right\}$

$a_n=\dfrac{3}{2^n}$

The numerator of all of these terms is $3$ and the denominators are the powers of $2$. So the sequence is: \[ a_n=\dfrac{3}{2^n} \]

ad
$\left\{\dfrac{1}{4},\dfrac{2}{9},\dfrac{3}{16},\dfrac{4}{25},\dfrac{5}{36}\right\}$

$a_n=\dfrac{n}{(n+1)^2}$

The numerator of all of these terms are the counting numbers $n$ and the denominators are perfect squares $(n+1)^2$. So the sequence is: \[ a_n=\dfrac{n}{(n+1)^2} \]

ad
$\left\{\dfrac{2}{1},\dfrac{4}{2},\dfrac{8}{6},\dfrac{16}{24},\dfrac{32}{120}\right\}$

Recall that $n$ factorial is
\[n!=n\cdot(n-1)\cdot(n-2)\cdot\cdots\cdot 3\cdot 2\cdot 1\]
and by definition $0!=1$.

$a_n=\dfrac{2^n}{n!}$

The numerator of all of these terms are the powers of $2$ and the denominators are the factorials starting with $1!$. So the sequence is: \[ a_n=\dfrac{2^n}{n!} \]

ad

In each problem, make a table of the first eight terms of each series and then plot these terms.

$a_n=\dfrac{2n-1}{n+1}$

$\begin{aligned} a_1 &= 1/2 \\ a_2 &= 1 \\ a_3 &= 5/4 \\ a_4 &= 7/5 \\ a_5 &= 9/6 \\ a_6 &= 11/7 \\ a_7 &= 13/8 \\ a_8 &= 15/9 \end{aligned}$
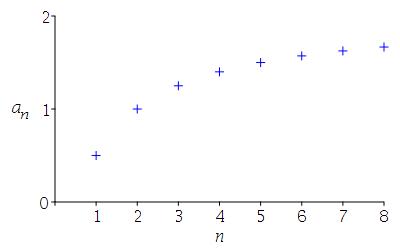
$b_n=\left\{3+\dfrac{(-1)^n}{n}\right\}$

$ \begin{aligned} b_1 &= 2 \\ b_2 &= 7/2 \\ b_3 &= 8/3 \\ b_4 &= 13/4 \\ b_5 &= 14/5 \\ b_6 &= 19/6 \\ b_7 &= 20/7 \\ b_8 &= 25/8 \end{aligned} $
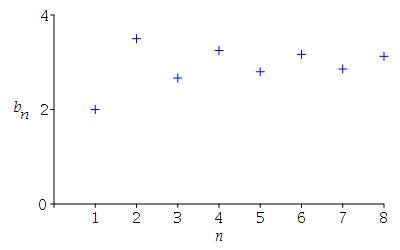
$c_n=2+(-1)^n$

$ \begin{aligned} c_1 &= 1 \\ c_2 &= 3 \\ c_3 &= 1 \\ c_4 &= 3 \\ c_5 &= 1 \\ c_6 &= 3 \\ c_7 &= 1 \\ c_8 &= 3 \end{aligned} $
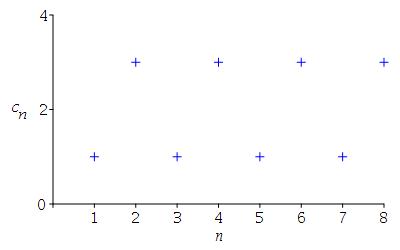
$d_n=\dfrac{2^n}{n!}$

$ \begin{aligned} d_1 &= 2 \\ d_2 &= 4/2!=2 \\ d_3 &= 8/3!=4/3 \\ d_4 &= 16/4!=2/3 \\ d_5 &= 32/5!=4/15 \\ d_6 &= 64/6!=4/45 \\ d_7 &= 128/7!=8/315 \\ d_8 &= 256/8!=2/315 \end{aligned} $

b. Limits of Sequences

In each problem, use a plot to guess the limit of the sequence. Then compute the limit exactly. If the limit does not exist, does the sequence approach positive or negative infinity?

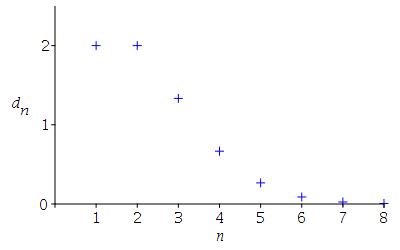
$a_n=\dfrac{3n-4}{4n-3}$ starting from $n=2$.

The limit appears to be between $.5$ and $1$. \[ \lim_{n\to\infty} a_n =\lim_{n\to\infty} \dfrac{3n-4}{4n-3} =\dfrac{3}{4} \]

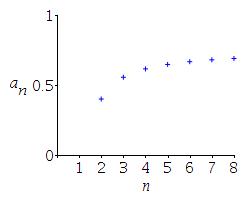
$ \begin{aligned} &a_2=\dfrac{3(2)-4}{4(2)-3}=\dfrac{2}{5}=0.4 \\ &a_3=\dfrac{3(3)-4}{4(3)-3}=\dfrac{5}{9}\approx0.56 \\ &a_4=\dfrac{3(4)-4}{4(4)-3}=\dfrac{8}{13}\approx0.62 \\ &a_5=\dfrac{3(5)-4}{4(5)-3}=\dfrac{11}{17}\approx0.65 \\ &a_6=\dfrac{3(6)-4}{4(6)-3}=\dfrac{2}{3}\approx0.67 \\ &a_7=\dfrac{3(7)-4}{4(7)-3}=\dfrac{17}{25}=0.68 \\ &a_8=\dfrac{3(8)-4}{4(8)-3}=\dfrac{20}{29}\approx0.69 \end{aligned} $

The limit appears to be between $.5$ and $1$. The actual limit is: \[ \lim_{n\to\infty} a_n =\lim_{n\to\infty}\dfrac{3n-4}{4n-3} =\lim_{n\to\infty}\dfrac{3-\dfrac{4}{n}}{4-\dfrac{3}{n}} =\dfrac{3}{4} \]
ad
$b_n=\arctan \left(\dfrac{\sqrt{3n+1}}{3\sqrt{n}+1}\right)$

The limit appears to be close to $.5$. \[ \lim_{n\to\infty} b_n =\lim_{n\to\theta}\arctan \dfrac{\sqrt{3n+1}}{3\sqrt{n}+1} =\dfrac{\pi}{6}\approx.524 \]

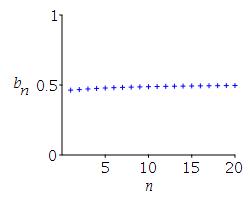
$ \begin{aligned} &b_1=\arctan \dfrac{\sqrt{3+1}}{3\sqrt{1}+1}\approx0.46 \\ &b_2=\arctan \dfrac{\sqrt{6+1}}{3\sqrt{2}+1}\approx0.47 \\ &b_3=\arctan \dfrac{\sqrt{9+1}}{3\sqrt{3}+1}\approx0.47 \\ &b_4=\arctan \dfrac{\sqrt{12+1}}{3\sqrt{4}+1}\approx0.48 \\ &b_5=\arctan \dfrac{\sqrt{15+1}}{3\sqrt{5}+1}\approx0.48 \\ &b_{10}=\arctan \dfrac{\sqrt{30+1}}{3\sqrt{10}+1}\approx0.49 \\ &b_{15}=\arctan \dfrac{\sqrt{45+1}}{3\sqrt{15}+1}\approx0.49 \\ &b_{20}=\arctan \dfrac{\sqrt{60+1}}{3\sqrt{20}+1}\approx0.5 \end{aligned} $

The limit appears to be close to $.5$. We compute: \[\begin{aligned} \lim_{n\to\infty} b_n &=\lim_{n\to\infty}\arctan \dfrac{\sqrt{3n+1}}{3\sqrt{n}+1} \\ &=\arctan\lim_{n\to\infty}\dfrac{\sqrt{3+\dfrac{1}{n}}} {3+\dfrac{1}{\sqrt{n}}} \\ &=\arctan\dfrac{\sqrt{3}}{3}=\dfrac{\pi}{6}\approx.524 \end{aligned}\]
ad
$c_n=\dfrac{n+\sin n}{2n+1}$

We would need to plot many more terms to feel safe in guessing that this sequence even has a limit and to estimate what that limit might be — though it seems plausible that the oscillations might grow smaller and smaller and approach $.5$. \[ \lim_{n\to\infty} c_n =\lim_{n\to\infty}\dfrac{n+\sin n}{2n+1}=\dfrac{1}{2} \]

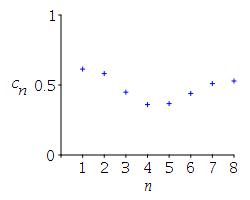
$ \begin{aligned} &c_1=\dfrac{1+\sin1}{2+1}\approx0.61 \\ &c_2=\dfrac{2+\sin2}{2(2)+1}\approx0.58 \\ &c_3=\dfrac{3+\sin3}{2(3)+1}\approx0.45 \\ &c_4=\dfrac{4+\sin4}{2(4)+1}\approx0.36 \\ &c_5=\dfrac{5+\sin5}{2(5)+1}\approx0.37 \\ &c_6=\dfrac{6+\sin6}{2(6)+1}\approx0.44 \\ &c_7=\dfrac{7+\sin7}{2(7)+1}\approx0.51 \\ &c_8=\dfrac{8+\sin8}{2(8)+1}\approx0.53 \end{aligned} $

It would require a much more extensive table to feel safe in guessing that this sequence even has a limit and to estimate what that limit might be — though it seems plausible that the oscillations might grow smaller and smaller and approach $.5$.

To compute the limit, we use the Sandwich Theorem: \[\begin{aligned} n-1 &\le n+\sin n \le n+1 \\ \dfrac{n-1}{2n+1} &\le \dfrac{n+\sin n}{2n+1} \le \dfrac{n+1}{2n+1} \end{aligned}\] Since $\displaystyle \lim_{n\to\infty}\dfrac{n-1}{2n+1} =\lim_{n\to\infty}\dfrac{n+1}{2n+1}=\dfrac{1}{2}$, we conclude: \[ \lim_{n\to\infty}\dfrac{n+\sin n}{2n+1} =\dfrac{1}{2} \]
ad
$d_n=\dfrac{n^2}{2n+1}$

We would surely guess that $\displaystyle \lim_{n\to\infty} d_n =\lim_{n\to\infty}\dfrac{n^2}{2n+1}=\infty$.
Indeed it is!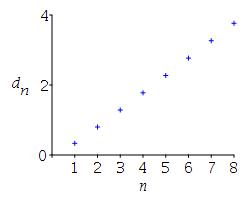

$\begin{aligned} &d_1=\dfrac{1^2}{2+1}=\dfrac{1}{3}\approx0.33 \\ &d_2=\dfrac{2^2}{2(2)+1}=\dfrac{4}{5}=0.8 \\ &d_3=\dfrac{3^2}{2(3)+1}=\dfrac{9}{7}\approx1.29 \\ &d_4=\dfrac{4^2}{2(4)+1}=\dfrac{16}{9}\approx1.78 \\ &d_5=\dfrac{5^2}{2(5)+1}=\dfrac{25}{11}\approx2.27 \\ &d_6=\dfrac{6^2}{2(6)+1}=\dfrac{36}{13}\approx2.77 \\ &d_7=\dfrac{7^2}{2(7)+1}=\dfrac{49}{15}\approx3.27 \\ &d_8=\dfrac{8^2}{2(8)+1}=\dfrac{64}{17}\approx3.76 \end{aligned}$

We would surely guess that $\displaystyle\lim_{n\to\infty}\dfrac{n^2}{2n+1}=\infty$. Indeed: \[ \lim_{n\to\infty}\dfrac{n^2}{2n+1} =\lim_{n\to\infty}\dfrac{n}{2+\dfrac{1}{n}}=\infty \]

ad
$a_n=\left(1+\dfrac{1}{n}\right)^n$

From the plot we could guess the limit to be about $2.6$. \[\lim_{n\to\infty}\left(1+\dfrac{1}{n}\right)^n=e\approx2.718\]

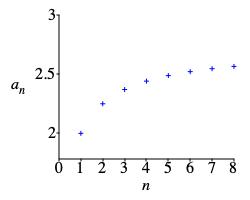
$ \begin{aligned} &a_1=\left(1+\dfrac{1}{1}\right)^1=2 \\ &a_2=\left(1+\dfrac{1}{2}\right)^2=2.25 \\ &a_3=\left(1+\dfrac{1}{3}\right)^3\approx2.37 \\ &a_4=\left(1+\dfrac{1}{4}\right)^4\approx2.44 \\ &a_6=\left(1+\dfrac{1}{6}\right)^6\approx2.52 \\ &a_8=\left(1+\dfrac{1}{8}\right)^8\approx2.57 \\ &a_{10}=\left(1+\dfrac{1}{10}\right)^{10}\approx2.59 \end{aligned} $

From the plot we could guess the limit to be about $2.6$. To compute the limit, we insert an $e^{\ln}$, move the limit inside the exponential and move an exponent out of the log: \[ \lim_{n\to\infty}\left(1+\dfrac{1}{n}\right)^n =\lim_{n\to\infty}{\large e}^{\scriptstyle \ln\left(1+\frac{\scriptstyle 1}{\scriptstyle n}\right)^n} ={\large e}^{\scriptstyle \lim\limits_{n\to\infty} n\ln\left(1+\frac{\scriptstyle 1}{\scriptstyle n}\right)} \] Now $\displaystyle\lim_{n\to\infty}n\ln\left(1+\dfrac{1}{n}\right)$ is of the form $\infty\cdot0$, so we write it as $\displaystyle\lim_{n\to\infty} \dfrac{\ln\left(1+\dfrac{1}{n}\right)}{\dfrac{1}{n}}$ which has the form $\dfrac{0}{0}$ and then we can use l'Hospital's Rule: \[\begin{aligned} \lim_{n\to\infty} \dfrac{\ln\left(1+\dfrac{1}{n}\right)}{\dfrac{1}{n}} &\overset{\text{l'H}}=\lim_{n\to\infty} \dfrac{\dfrac{1}{1+\frac{1}{n}}(-n^{-2})}{-n^{-2}} \\ &=\lim_{n\to\infty} \left(1+\dfrac{1}{n}\right)=1 \end{aligned}\] Therefore: \[ \lim_{n\to\infty}\left(1+\dfrac{1}{n}\right)^n=e^1=e \]
ad
$b_n=\dfrac{n^2}{2^n}$

Apply L'Hospital's rule twice.

From the plot, we guess the limit to be $0$. In fact, \[\lim_{n\to\infty}\dfrac{n^2}{2^n}=0\]

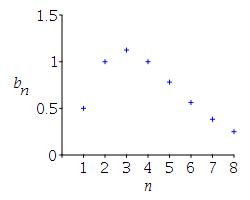
$\begin{aligned} &b_1=\dfrac{1^2}{2^1}=\dfrac{1}{2}=0.5 \\ &b_2=\dfrac{2^2}{2^2}=\dfrac{4}{4}=1 \\ &b_3=\dfrac{3^2}{2^3}=\dfrac{9}{8}=1.125 \\ &b_4=\dfrac{4^2}{2^4}=\dfrac{16}{16}=1 \\ &b_5=\dfrac{5^2}{2^5}=\dfrac{25}{32}\approx0.781 \\ &b_6=\dfrac{6^2}{2^6}=\dfrac{36}{64}\approx0.563 \\ &b_7=\dfrac{7^2}{2^7}=\dfrac{49}{128}\approx0.383 \\ &b_8=\dfrac{8^2}{2^8}=\dfrac{64}{256}=0.25 \\ \end{aligned}$

From the plot we could guess the limit to be $0$. The limit has form $\dfrac{\infty}{\infty}$, so we apply l'Hospital's rule: \[ \lim\limits_{n\to\infty}\dfrac{n^2}{2^n}\overset{\text{l'H}} =\lim\limits_{n\to\infty}\dfrac{2n}{2^n\ln(2)} \] The new limit still has the form $\dfrac{\infty}{\infty}$! So we apply l'Hospital's rule again. \[ \lim\limits_{n\to\infty}\dfrac{n^2}{2^n}\overset{\text{l'H}} =\lim\limits_{n\to\infty}\dfrac{2}{2^n[\ln(2)]^2}=0 \]
ad

In each problem, determine if the sequence is convergent or divergent, If it converges, find the limit. If it diverges, determine if it diverges to plus infinity or minus infinity or is oscillatory divergent?
Be sure to read the four remarks!

$\left(\dfrac{3}{4}\right)^n$

$\lim\limits_{n\to\infty}\left(\dfrac{3}{4}\right)^n=0$

We first change the base from $\dfrac{3}{4}$ to $e$ and pull the exponential function out:
\[ \lim_{n\to\infty}\left(\dfrac{3}{4}\right)^n= \lim_{n\to\infty}{\large e}^{\scriptstyle n\ln(3/4)}= {\large e}^{\scriptstyle \lim\limits_{n\to\infty}n\ln(3/4)} \]
Notice that $\ln\left(\dfrac{3}{4}\right)$ is negative. That means $\lim\limits_{n\to\infty}n\ln\left(\dfrac{3}{4}\right)$ diverges to $-\infty$ and therefore: \[ \lim_{n\to\infty}\left(\dfrac{3}{4}\right)^n={\large e}^{-\infty}=0 \]
ad

The same argument shows that $\lim\limits_{n\to\infty} r^n=0$ for any $r$ satisfying $0 \lt r \lt 1$.
In the future, it is sufficient to just quote this result.
$\left(\dfrac{-3}{4}\right)^n$

$\lim\limits_{n\to\infty}\left(\dfrac{-3}{4}\right)^n=0$

We first split the limit as a product: \[ \lim_{n\to\infty}\left(\dfrac{-3}{4}\right)^n= \lim_{n\to\infty}(-1)^n\left(\dfrac{3}{4}\right)^n \] Since: \[ -1 \le (-1)^n \le 1 \] we conclude: \[ -\left(\dfrac{3}{4}\right)^n \le (-1)^n\left(\dfrac{3}{4}\right)^n \le \left(\dfrac{3}{4}\right)^n \] By the previous problem: \[ \lim_{n\to\infty}\left(\dfrac{3}{4}\right)^n=0 \] So we also have: \[ \lim_{n\to\infty}-\left(\dfrac{3}{4}\right)^n=-0=0 \] By the Sandwich Theorem, we conclude: \[ \lim_{n\to\infty}\left(\dfrac{-3}{4}\right)^n=0 \] also.
ad

The same argument shows that $\lim\limits_{n\to\infty} r^n=0$ for any $r$ satisfying $-1 \lt r \lt 0$.
In the future, it is sufficient to just quote this result.
$\left(\dfrac{4}{3}\right)^n$

$\lim\limits_{n\to\infty}\left(\dfrac{4}{3}\right)^n$ diverges to $+\infty$.

We first change the base from $\dfrac{4}{3}$ to $e$ and pull the exponential function out:
\[ \lim_{n\to\infty}\left(\dfrac{4}{3}\right)^n= \lim_{n\to\infty}{\large e}^{\scriptstyle \ln(4/3)^n}= {\large e}^{\scriptstyle \lim\limits_{n\to\infty}n\ln(4/3)} \]
Since $\ln\left(\dfrac{4}{3}\right)$ is positive, $\lim\limits_{n\to\infty} n\ln\left(\dfrac{4}{3}\right)$ diverges to $+\infty$ and therefore: \[ \lim_{n\to\infty}\left(\dfrac{3}{4}\right)^n={\large e}^{\infty}=\infty \]
ad

The same argument shows that $\lim\limits_{n\to\infty} r^n=\infty$ for any $r$ satisfying $r \gt 1$.
In the future, it is sufficient to just quote this result.
$\left(\dfrac{-4}{3}\right)^n$

$\displaystyle \lim_{n\to\infty}\left(\dfrac{-4}{3}\right)^n$ is oscillatory divergent.
The odd-numbered terms $\to-\infty$, while the even-numbered ones $\to+\infty$.

We first look at the even numbered terms: \[ \lim_{n\to\infty}\left(\dfrac{-4}{3}\right)^{2n} =\lim_{n\to\infty}\left(\dfrac{16}{9}\right)^n=\infty \] We next look at the odd numbered terms: \[ \lim_{n\to\infty}\left(\dfrac{-4}{3}\right)^{2n+1} =\dfrac{-4}{3}\lim_{n\to\infty}\left(\dfrac{16}{9}\right)^n=-\infty \] So $\left(\dfrac{-4}{3}\right)^n$ oscillates between large positive and large negative numbers. So the sequence is oscillatory divergent.
ad

The same argument shows that $\lim\limits_{n\to\infty} r^n$ is oscillatory divergent for any $r$ satisfying $r \lt -1$.
In the future, it is sufficient to just quote this result.

$\dfrac{3n^2-4n+1}{n^2-4n+3}$

Divide the numerator and denominator by $n^2$.

$\displaystyle \lim_{n\to\infty}\dfrac{3n^2-4n+1}{n^2-4n+3}=3$

We divide the numerator and denominator by $n^2$:
\[ \lim_{n\to\infty}\dfrac{3n^2-4n+1}{n^2-4n+3}= \lim_{n\to\infty}\dfrac{3-\dfrac{4}{n}+\dfrac{1}{n^2}}{1-\dfrac{4}{n}+\dfrac{3}{n^2}}= \lim_{n\to\infty}\dfrac{3}{1}=3 \]
ad
$\dfrac{\ln(3+e^n)}{2n}$

Apply l'Hospital's rule.

$\lim\limits_{n\to\infty}\dfrac{\ln(3+e^n)}{2n}=\dfrac{1}{2}$

The limit is in the form of $\dfrac{\infty}{\infty}$, so we apply l'Hospital's rule: \[\begin{aligned} \lim_{n\to\infty}&\dfrac{\ln(3+e^n)}{2n} \overset{\text{l'H}}=\lim_{n\to\infty}\dfrac{\dfrac{e^n}{3+e^n}}{2} \\ &=\lim_{n\to\infty}\dfrac{e^n}{6+2e^n} =\lim_{n\to\infty}\dfrac{1}{6e^{-n}+2}=\dfrac{1}{2} \end{aligned}\]
ad
$\dfrac{1+(-1)^n n}{1+2n}$

$\displaystyle \lim_{n\to\infty}\dfrac{1+(-1)^n n}{1+2n}$ is oscillatory divergent. Half the terms approach $\dfrac{1}{2}$, the other half approach $-\dfrac{1}{2}$.

We divide the numerator and denominator by $n$: \[ \lim_{n\to\infty}\dfrac{1+(-1)^n n}{1+2n}= \lim_{n\to\infty}\dfrac{\dfrac{1}{n}+(-1)^n}{\dfrac{1}{n}+2} \] Now $\lim\limits_{n\to\infty}\dfrac{1}{n}=0$ and $\lim\limits_{n\to\infty}\dfrac{(-1)^n}{2}$ oscillates between $-\, \dfrac{1}{2}$ and $\dfrac{1}{2}$ and never approaches any value.
Therefore $\lim\limits_{n\to\infty}\dfrac{1+(-1)^n n}{1+2n}$ is oscillatory divergent.
ad
$\dfrac{1+2n-3n^2}{2-4n+n^2}$

Divide the numerator and denominator by $n^2$.

$\displaystyle \lim_{n\to\infty}\dfrac{1+2n-3n^2}{2-4n+n^2}=-3$

We divide the numerator and denominator by $n^2$: \[ \lim_{n\to\infty}\dfrac{1+2n-3n^2}{2-4n+n^2}= \lim_{n\to\infty}\dfrac{\dfrac{1}{n^2}+\dfrac{2}{n}-3}{\dfrac{2}{n^2}-\dfrac{4}{n}+1}= -3 \]
ad
$\dfrac{1+2n-3n^2}{2+4n}$

Divide the numerator and denominator by $n$.

$\displaystyle \lim_{n\to\infty}\dfrac{1+2n-3n^2}{2+4n}$ diverges to $-\infty$.

We divide the numerator and denominator by $n$: \[\begin{aligned} \lim_{n\to\infty}&\dfrac{1+2n-3n^2}{2+4n} =\lim_{n\to\infty}\dfrac{\dfrac{1}{n}+2-3n}{\dfrac{2}{n}+4} \\ &=\lim_{n\to\infty}\dfrac{2-3n}{4} =-\infty \end{aligned}\]
ad
$\left(1+\dfrac{3}{n}\right)^{4n}$

$\lim\limits_{n\to\infty}\left(1+\dfrac{3}{n}\right)^{4n}=e^{12}$

The limit has form $1^\infty$, so we insert an $e^{\ln}$ into the limit, move the limit inside the exponential and move the exponent out of the log: \[ \lim_{n\to\infty}\left(1+\dfrac{3}{n}\right)^{4n} =\lim_{n\to\infty} {\large e}^{\scriptstyle \ln\left(1+\frac{\scriptstyle 3}{\scriptstyle n}\right)^{\scriptstyle 4n}} ={\large e}^{\scriptstyle \lim\limits_{n\to\infty} 4n\ln{\scriptstyle \left(1+\frac{\scriptstyle 3}{\scriptstyle n}\right)}} \] Now $\displaystyle\lim_{n\to\infty}4n\ln\left(1+\dfrac{3}{n}\right)$ is of the form $\infty\cdot0$, so we write it as $\displaystyle \lim_{n\to\infty} \dfrac{\ln\left(1+\dfrac{3}{n}\right)}{\dfrac{1}{4n}}$ which has the form $\dfrac{0}{0}$ and then we can use l'Hospital's rule: \[\begin{aligned} \lim_{n\to\infty}\dfrac{\ln\left(1+\dfrac{3}{n}\right)}{\dfrac{1}{4n}} &\overset{\text{l'H}}= \lim_{n\to\infty}\dfrac{\dfrac{1}{1+\dfrac{3}{n}}(-3n^{-2})}{\dfrac{1}{4}(-n^{-2})} \\ \end{aligned}\] \[\begin{aligned} &=\lim_{n\to\infty}\dfrac{12}{1+\dfrac{3}{n}}=12 \end{aligned}\] Therefore: \[ \lim_{n\to\infty}\left(1+\dfrac{3}{n}\right)^{4n}=e^{12} \]
ad

Can you find a general formula for \[ \lim_{n\to\infty}\left(1+\dfrac{a}{n}\right)^{bn} ? \]
$\left(1+\dfrac{1}{n^2}\right)^n$

$\lim\limits_{n\to\infty}\left(1+\dfrac{1}{n^2}\right)^n=1$

The limit has form $1^\infty$, so we insert an $e^{\ln}$ into the limit, move the limit inside the exponential and move the exponent out of the log: \[ \lim_{n\to\infty}\left(1+\dfrac{1}{n^2}\right)^n =\lim_{n\to\infty}{\large e}^{\scriptstyle \ln\left(1+\frac{\scriptstyle 1}{\scriptstyle n^2}\right)^{\scriptstyle n}} ={\large e}^{\scriptstyle \lim\limits_{n\to\infty}n\ln{\scriptstyle \left(1+\frac{\scriptstyle 1}{\scriptstyle n^2}\right)}} \] Now $\displaystyle\lim_{n\to\infty}n\ln\left(1+\frac{1}{n^2}\right)$ is of the form $\infty\cdot0$, so we write it as $\displaystyle \lim_{n\to\infty}\dfrac{\ln\left(1+\dfrac{1}{n^2}\right)}{\dfrac{1}{n}}$ which has the form $\dfrac{0}{0}$ and then we can use l'Hospital's rule: \[ \lim_{n\to\infty}\dfrac{\ln\left(1+\dfrac{1}{n^2}\right)}{\dfrac{1}{n}} \overset{\text{l'H}}= \lim_{n\to\infty}\dfrac{\dfrac{1}{1+\dfrac{1}{n^2}}(-2n^{-3})}{-n^{-2}}= \lim_{n\to\infty}\dfrac{\dfrac{2}{n}}{1+\dfrac{1}{n^2}}=0 \] Therefore: \[ \lim\limits_{n\to\infty} \left(1+\dfrac{1}{n^2}\right)^n =e^0=1 \]
ad
$\left(1+\dfrac{1}{n}\right)^{n^2}$

$\lim\limits_{n\to\infty}\left(1+\dfrac{1}{n}\right)^{n^2}$ diverges to $+\infty$

The limit has form $1^\infty$, so we insert an $e^{\ln}$ into the limit, move the limit inside the exponential and move the exponent out of the log: \[ \lim_{n\to\infty}\left(1+\dfrac{1}{n}\right)^{n^2} =\lim_{n\to\infty}{\large e}^{\scriptstyle \ln\left(1+\frac{\scriptstyle 1}{\scriptstyle n}\right)^{\scriptstyle n^2}} ={\large e}^{\scriptstyle \lim\limits_{n\to\infty}n^2\ln{\scriptstyle \left(1+\frac{\scriptstyle 1}{\scriptstyle n}\right)}} \] Now $\displaystyle\lim_{n\to\infty}n^2\ln\left(1+\dfrac{1}{n}\right)$ is of the form $\infty\cdot0$, so we write it as $\displaystyle \lim_{n\to\infty}\dfrac{\ln\left(1+\dfrac{1}{n}\right)}{\dfrac{1}{n^2}}$ which has the form $\dfrac{0}{0}$ and then we can use l'Hospital's rule: \[ \lim_{n\to\infty}\dfrac{\ln\left(1+\dfrac{1}{n}\right)}{\dfrac{1}{n^2}} \overset{\text{l'H}}= \lim_{n\to\infty}\dfrac{\dfrac{1}{1+\dfrac{1}{n}}(-n^{-2})}{-2n^{-3}}= \lim_{n\to\infty}\dfrac{n}{2+\dfrac{2}{n}}=\infty \] Therefore: \[ \lim_{n\to\infty}\left(1+\dfrac{1}{n}\right)^{n^2} =e^\infty=\infty \]
ad

c. Bounded and Monotonic Sequences

In each problem, determine if the sequence is increasing, decreasing or not monotonic. Also determine if it is bounded above, below, both or neither.

$a_n=n+\sin\left(\dfrac{n\pi}{2}\right)$

Sequence is increasing but not strictly increasing.
It is bounded below by $2$ and unbounded above.

To determine if the sequence is monotonic, we write out the first $12$ terms of the sequence $a_n=n+\sin\left(\dfrac{n\pi}{2}\right)$: \[\begin{aligned} &a_1=1+\sin\left(\dfrac{\pi}{2}\right)=2\\ &a_2=2+\sin\left(\pi\right)=2\\ &a_3=3+\sin\left(\dfrac{3\pi}{2}\right)=2\\ &a_4=4+\sin\left(2\pi\right)=4\\ &a_5=5+\sin\left(\dfrac{5\pi}{2}\right)=6\\ &a_6=6+\sin\left(3\pi\right)=6\\ &a_7=7+\sin\left(\dfrac{7\pi}{2}\right)=6\\ &a_8=8+\sin\left(4\pi\right)=8\\ &a_9=9+\sin\left(\dfrac{9\pi}{2}\right)=10\\ &a_{10}=10+\sin\left(5\pi\right)=10\\ &a_{11}=11+\sin\left(\dfrac{11\pi}{2}\right)=10\\ &a_{12}=12+\sin\left(6\pi\right)=12 \end{aligned}\] So the sequence is increasing but not strictly increasing. Also, the lower bound is $2$. There is also no upper bound because the sequence $a_n=n$ is unbounded above while the sequence $a_n=\sin\left(\dfrac{n\pi}{2}\right)$ is bounded above by $1$ and bounded below by $-1$.
ad
$a_n=-2n+\sin\left(\dfrac{n\pi}{2}\right)$

The sequence is strictly decreasing, bounded above by $-1$, unbounded below.

To figure out if the sequence is monotonic, we write out the first $6$ terms of the sequence $a_n=-2n+\sin\left(\dfrac{n\pi}{2}\right)$: \[\begin{aligned} &a_1=-2+\sin\left(\dfrac{\pi}{2}\right)=-1\\ &a_2=-4+\sin\left(\pi\right)=-4\\ &a_3=-6+\sin\left(\dfrac{3\pi}{2}\right)=-7\\ &a_4=-8+\sin\left(2\pi\right)=-8\\ &a_5=-10+\sin\left(\dfrac{5\pi}{2}\right)=-9\\ &a_6=-12+\sin\left(3\pi\right)=-12 \end{aligned}\] So we suspect the sequence is strictly decreasing.

To prove this rigorously we separately check $a_n \gt a_{n+1}$ when $n$ is each of the forms $4m$, $4m+1$, $4m+2$, or $4m+3$ for some non-negative integer $m$. \[\begin{aligned} &\text{If}\;n=4m,\,\text{then} \\ &\qquad a_{4m}-2(4m)+\sin\left(\dfrac{(4m)\pi}{2}\right)=-8m \\ &\text{If}\;n=4m+1,\,\text{then} \\ &\qquad a_{4m+1}-2(4m+1)+\sin\left(\dfrac{(4m+1)\pi}{2}\right)=-8m-1 \\ &\text{If}\;n=4m+2,\,\text{then} \\ &\qquad a_{4m+2}-2(4m+2)+\sin\left(\dfrac{(4m+2)\pi}{2}\right)=-8m-4 \\ &\text{If}\;n=4m+3,\,\text{then} \\ &\qquad a_{4m+3}-2(4m+3)+\sin\left(\dfrac{(4m+3)\pi}{2}\right)=-8m-7 \\ &\text{If}\;n=4m+4,\,\text{then} \\ &\qquad a_{4m+4}-2(4m+4)+\sin\left(\dfrac{(4m+4)\pi}{2}\right)=-8m-8 \end{aligned}\] Since: \[\begin{aligned} -8m \gt -8m-1 \gt -8m-4 \gt -8m-7 \gt -8m-8 \end{aligned}\] the sequence is strictly decreasing in each group of $4$ terms. There is no lower bound because the sequence $a_n=-2n$ is unbounded below while the sequence $a_n=\sin\left(\dfrac{n\pi}{2}\right)$ is bounded between $1$ and $-1$. Also, the upper bound is $-1$.
ad

$a_n=\dfrac{n+\sin\left(\dfrac{n\pi}{2}\right)}{n}$

Sequence is not monotonic (but converges to $1$). It is bounded above by $2$ and below by $\dfrac{2}{3}$.

We first rewrite the series as: \[ a_n=\dfrac{n+\sin\left(\dfrac{n\pi}{2}\right)}{n} =1+\dfrac{\sin\left(\dfrac{n\pi}{2}\right)}{n} \] The function $\sin\left(\dfrac{n\pi}{2}\right)$ cycles between $1$, $0$, $-1$ and $0$. So the sequence $a_n$ cycles between $1+\dfrac{1}{n}$, $1$, $1-\dfrac{1}{n}$ and $1$ with $\dfrac{1}{n}$ getting smaller:

\[\begin{aligned} &a_1=1+\dfrac{1}{1}=2 \quad &a_2=1 \\ &a_3=1-\dfrac{1}{3}=\dfrac{2}{3} \quad &a_4=1 \\ &a_5=1+\dfrac{1}{5}=\dfrac{6}{5} \quad &a_6=1 \\ &a_7=1-\dfrac{1}{7}=\dfrac{6}{7} \quad &a_8=1 \\ &a_9=1+\dfrac{1}{9}=\dfrac{10}{9} \quad &a_{10}=1 \end{aligned}\]

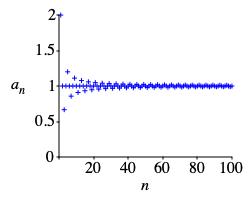
So the sequence is not monotonic but converges to $1$. Further, it is bounded above by the first term $a_1=2$ and below by the second term $a_3=\dfrac{2}{3}$.

ad
$a_n=\dfrac{-2n+\sin\left(\dfrac{n\pi}{2}\right)}{n}$

Sequence is not monotonic (but converges to $-2$). It is bounded above by $-1$ and below by $-\,\dfrac{7}{3}$.

We first rewrite the series as: \[ a_n=\dfrac{n+\sin\left(\dfrac{n\pi}{2}\right)}{n} =-2+\dfrac{\sin\left(\dfrac{n\pi}{2}\right)}{n} \] The function $\sin\left(\dfrac{n\pi}{2}\right)$ cycles between $1$, $0$, $-1$ and $0$. So the sequence $a_n$ cycles between $-2+\dfrac{1}{n}$, $-2$, $-2-\dfrac{1}{n}$ and $-2$ with $\dfrac{1}{n}$ getting smaller: \[\begin{aligned} &a_1=-2+\dfrac{1}{1}=-1 \quad &a_2=-2 \\ &a_3=-2-\dfrac{1}{3}=-\,\dfrac{7}{3} \quad &a_4=-2 \\ &a_5=-2+\dfrac{1}{5}=-\,\dfrac{9}{5} \quad &a_6=-2 \\ &a_7=-2-\dfrac{1}{7}=-\,\dfrac{15}{7} \quad &a_8=-2 \\ &a_9=-2+\dfrac{1}{9}=-\,\dfrac{17}{9} \quad &a_{10}=-2 \end{aligned}\] So the sequence is not monotonic but converges to $-2$. Further, it is bounded above by the first term $a_1=-1$ and below by the second term $a_3=-\,\dfrac{7}{3}$.

ad

d. Recursively Defined Sequences

In each problem, write out the first five terms of the sequence, determine if the sequence is bounded and/or monotonic. Then use the Bounded, Monotonic Sequence Theorem to determine whether the sequence converges. If it converges, find find the limit. If it diverges, determine if it diverges to $\infty$ or $-\infty$ or is oscillatory divergent.

$a_1=2,\qquad a_{n+1}=2\sqrt{a_n}$

$\begin{aligned} a_1&=2\qquad a_{n+1}=2\sqrt{a_n} \\ a_2&=2\sqrt{2}=2.828 \\ a_3&=2\sqrt{2\sqrt{2}}=3.364 \\ a_4&=2\sqrt{2\sqrt{2\sqrt{2}}}=3.67 \\ a_5&=2\sqrt{2\sqrt{2\sqrt{2\sqrt{2}}}}=3.83 \\ \end{aligned}$
The sequence is increasing and bounded above by $4$.
$\displaystyle \lim_{n\to\infty} a_n=4$.

\[\begin{aligned} a_1&=2\qquad a_{n+1}=2\sqrt{a_n} \\ a_2&=2\sqrt{2}=2.828 \\ a_3&=2\sqrt{2\sqrt{2}}=3.364 \\ a_4&=2\sqrt{2\sqrt{2\sqrt{2}}}=3.67 \\ a_5&=2\sqrt{2\sqrt{2\sqrt{2\sqrt{2}}}}=3.83 \\ \end{aligned}\] The sequence appears to be increasing and bounded above by $4$.
We first assume the sequence has a limit and find the possible limits.
Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\displaystyle\lim_{n\to\infty}a_{n+1}=L$ also. Taking limits of both sides of the recursion relation gives \[\begin{aligned} &\lim_{n\to\infty} a_{n+1}=\lim_{n\to\infty} 2\sqrt{a_n} \quad \Rightarrow \quad L=2\sqrt{L} \\ &\Rightarrow \quad L^2=4L \quad \Rightarrow \quad L(L-4)=0 \\ &\Rightarrow \quad L=0,4 \\ \end{aligned}\] So if the sequence has a limit, it must be $0$ or $4$. Looking at the terms, we expect the limit is increasing to $4$.

We want to prove the sequence is increasing and bounded above by $4$ using mathematical induction. So we need to prove $a_n \lt a_{n+1} \lt 4$.
Initialization Step: $a_1 \lt a_2 \lt 4$ since $2 \lt 2\sqrt{2} \lt 4$.
Induction Step: Assume $a_k \lt a_{k+1} \lt 4$ and prove $a_{k+1} \lt a_{k+2} \lt 4$. \[\begin{aligned} &a_k \lt a_{k+1} \lt 4 \quad \Rightarrow \quad \sqrt{a_k} \lt \sqrt{a_{k+1}} \lt 2 \\ &\Rightarrow \quad 2\sqrt{a_k} \lt 2\sqrt{a_{k+1}} \lt 4 \quad \Rightarrow \quad a_{k+1} \lt a_{k+2} \lt 4 \end{aligned}\] Hence the sequence is increasing from $2$ and bounded above by $4$. So by the Bounded, Monotonic Sequence Theorem the sequence converges to: \[ \lim_{n\to\infty} a_n=4 \]
ad
$a_1=5,\qquad a_{n+1}=2\sqrt{a_n}$

$\begin{aligned} a_1&=5,\qquad a_{n+1}=2\sqrt{a_n} \\ a_2&=2\sqrt{5}=4.472 \\ a_3&=2\sqrt{2\sqrt{5}}=4.23 \\ a_4&=2\sqrt{2\sqrt{2\sqrt{5}}}=4.11 \\ a_5&=2\sqrt{2\sqrt{2\sqrt{2\sqrt{5}}}}=4.06 \\ \end{aligned}$
The sequence is decreasing for all $n$.

The sequence is bounded below by $4$ and above by $5$.

$\displaystyle\lim_{n\to\infty}a_n=4$.

\[\begin{aligned} a_1&=5,\qquad a_{n+1}=2\sqrt{a_n} \\ a_2&=2\sqrt{5}=4.472 \\ a_3&=2\sqrt{2\sqrt{5}}=4.23 \\ a_4&=2\sqrt{2\sqrt{2\sqrt{5}}}=4.11 \\ a_5&=2\sqrt{2\sqrt{2\sqrt{2\sqrt{5}}}}=4.06 \\ \end{aligned}\] The sequence appears to be decreasing and bounded below by $4$.
We first assume the sequence has a limit and find the possible limits.
Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\displaystyle\lim_{n\to\infty}a_{n+1}=L$ also. Taking limits of both sides of the recursion relation gives \[\begin{aligned} &\lim_{n\to\infty} a_{n+1}=\lim_{n\to\infty} 2\sqrt{a_n} \quad \Rightarrow \quad L=2\sqrt{L} \\ &\Rightarrow \quad L^2=4L \quad \Rightarrow \quad L(L-4)=0 \\ &\Rightarrow \quad L=0,4 \\ \end{aligned}\] So if the sequence has a limit, it must be $0$ or $4$. Looking at the terms, we expect the limit is decreasing to $4$.

We want to prove the sequence is decreasing and bounded below by $4$ using mathematical induction. So we need to prove $a_n \gt a_{n+1} \gt 4$.
Initialization Step: $a_1 \gt a_2 \gt 4$ since $5 \gt 2\sqrt{5} \gt 4$.
Induction Step: Assume $a_k \gt a_{k+1} \gt 4$ and prove $a_{k+1} \gt a_{k+2} \gt 4$. \[\begin{aligned} &a_k \gt a_{k+1} \gt 4 \quad \Rightarrow \quad \sqrt{a_k} \gt \sqrt{a_{k+1}} \gt 2 \\ &\Rightarrow \quad 2\sqrt{a_k} \gt 2\sqrt{a_{k+1}} \gt 4 \quad \Rightarrow \quad a_{k+1} \gt a_{k+2} \gt 4 \end{aligned}\] Hence the sequence is decreasing from $5$ and bounded below by $4$. So by the Bounded, Monotonic Sequence Theorem the sequence converges to: \[ \lim_{n\to\infty} a_n=4 \]
ad

Notice that this and the previous problem have the same recusion relation but different initial terms. The limits are the same. One increases to the limit and the other decreases to the limit.
$a_1=2,\qquad a_{n+1}=\dfrac{1}{3}(a_n)^2$

$\begin{aligned} a_1&=2,\qquad a_{n+1}=\dfrac{1}{3}(a_n)^2 \\ a_2&=\dfrac{1}{3}(2)^2=1.33 \\ a_3&=\dfrac{1}{3}\left(\dfrac{1}{3}(2)^2\right)^2=.593 \\ a_4&=\dfrac{1}{3}\left(\dfrac{1}{3} \left(\dfrac{1}{3}(2)^2\right)^2\right)^2=.117 \\ a_5&=\dfrac{1}{3}\left(\dfrac{1}{3} \left(\dfrac{1}{3}\left(\dfrac{1}{3}(2)^2\right)^2\right)^2\right)^2=.0046 \\ \end{aligned}$
The sequence is decreasing and bounded below by $0$.

$\displaystyle\lim_{n\to\infty}a_n=0$.

\[\begin{aligned} a_1&=2,\qquad a_{n+1}=\dfrac{1}{3}(a_n)^2 \\ a_2&=\dfrac{1}{3}(2)^2=1.33 \\ a_3&=\dfrac{1}{3}\left(\dfrac{1}{3}(2)^2\right)^2=.593 \\ a_4&=\dfrac{1}{3}\left(\dfrac{1}{3} \left(\dfrac{1}{3}(2)^2\right)^2\right)^2=.117 \\ a_5&=\dfrac{1}{3}\left(\dfrac{1}{3} \left(\dfrac{1}{3}\left(\dfrac{1}{3}(2)^2\right)^2\right)^2\right)^2=.0046 \\ \end{aligned}\] The sequence appears to be decreasing and bounded below by $0$.
We first assume the sequence has a limit and find the possible limits.
Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\displaystyle\lim_{n\to\infty}a_{n+1}=L$ also. Taking limits of both sides of the recursion relation gives \[\begin{aligned} &\lim_{n\to\infty} a_{n+1}=\lim_{n\to\infty} \dfrac{1}{3}(a_n)^2 \quad \Rightarrow \quad L=\dfrac{1}{3}(L)^2 \\ &\Rightarrow \quad L^2-3L=0 \quad \Rightarrow \quad L(L-3)=0 \\ &\Rightarrow \quad L=0,3 \\ \end{aligned}\] So if the sequence has a limit, it must be $0$ or $3$. Looking at the terms, we expect the limit is decreasing to $0$.

We want to prove the sequence is decreasing and bounded below by $0$ using mathematical induction. So we need to prove $a_n \gt a_{n+1} \gt 0$.
Initialization Step: $a_1 \gt a_2 \gt 0$ since $2 \gt \dfrac{4}{3} \gt 0$.
Induction Step: Assume $a_k \gt a_{k+1} \gt 0$ and prove $a_{k+1} \gt a_{k+2} \gt 0$. \[\begin{aligned} &a_k \gt a_{k+1} \gt 0 \quad \Rightarrow \quad {a_k}^2 \gt {a_{k+1}}^2 \gt 0 \\ &\Rightarrow \quad \dfrac{1}{3}{a_k}^2 \gt \dfrac{1}{3}{a_{k+1}}^2 \gt 0 \quad \Rightarrow \quad a_{k+1} \gt a_{k+2} \gt 0 \end{aligned}\] Hence the sequence is decreasing from $2$ and bounded below by $0$. So by the Bounded, Monotonic Sequence Theorem the sequence converges to: \[ \lim_{n\to\infty} a_n=0 \]
ad
$a_1=4,\qquad a_{n+1}=\dfrac{1}{3}(a_n)^2$

$\begin{aligned} a_1&=4,\qquad a_{n+1}=\dfrac{1}{3}(a_n)^2 \\ a_2&=\dfrac{1}{3}(4)^2=5.33 \\ a_3&=\dfrac{1}{3}\left(\dfrac{1}{3}(4)^2\right)^2=9.48 \\ a_4&=\dfrac{1}{3}\left(\dfrac{1}{3} \left(\dfrac{1}{3}(4)^2\right)^2\right)^2=29.97 \\ a_5&=\dfrac{1}{3}\left(\dfrac{1}{3} \left(\dfrac{1}{3}\left(\dfrac{1}{3}(4)^2\right)^2\right)^2\right)^2=299.4 \\ \end{aligned}$
The sequence is increasing and unbounded.

$\displaystyle\lim_{n\to\infty}a_n=\infty$.

\[\begin{aligned} a_1&=4,\qquad a_{n+1}=\dfrac{1}{3}(a_n)^2 \\ a_2&=\dfrac{1}{3}(4)^2=5.33 \\ a_3&=\dfrac{1}{3}\left(\dfrac{1}{3}(4)^2\right)^2=9.48 \\ a_4&=\dfrac{1}{3}\left(\dfrac{1}{3} \left(\dfrac{1}{3}(4)^2\right)^2\right)^2=29.97 \\ a_5&=\dfrac{1}{3}\left(\dfrac{1}{3} \left(\dfrac{1}{3}\left(\dfrac{1}{3}(4)^2\right)^2\right)^2\right)^2=299.4 \\ \end{aligned}\] It appears that the sequence is increasing and diverges to $\infty$. The previous problem has the same recursion formula. There we found that if this sequence has a limit, that limit must be either $0$ or $3$, neither of which is possible here if we prove the sequence is increasing.

Let us use mathematical induction to show the sequence is increasing. So we need to prove $a_n \lt a_{n+1}$.
Initialization Step: $a_1 \lt a_2$ since $4 \lt \dfrac{16}{3}$.
Induction Step: Assume $a_k \lt a_{k+1}$ and prove $a_{k+1} \lt a_{k+2}$. \[\begin{aligned} &a_k \lt a_{k+1} \quad \Rightarrow \quad {a_k}^2 \lt {a_{k+1}}^2 \\ &\Rightarrow \quad \dfrac{1}{3}{a_k}^2 \lt \dfrac{1}{3}{a_{k+1}}^2 \quad \Rightarrow \quad a_{k+1} \lt a_{k+2} \end{aligned}\] Hence the sequence is increasing from $4$ and cannot have a limit greater than $3$. So by the Bounded, Monotonic Sequence Theorem the sequence is unbounded above and diverges to \[ \lim_{n\to\infty} a_n=\infty \]
ad

Notice that this and the previous problem have the same recusion relation but different initial terms. However the limits are not the same. One decreases to a $0$ limit and the other increases to infinity.
$a_1=2,\qquad a_{n+1}=\dfrac{1}{2}a_n+3$

$\begin{aligned} a_1&=2,\qquad a_{n+1}=\dfrac{1}{2}a_n+3 \\ a_2&=\dfrac{1}{2}(2)+3=4 \\ a_3&=\dfrac{1}{2}(4)+3=5 \\ a_4&=\dfrac{1}{2}(5)+3=\dfrac{5}{2}+3=5.5 \\ a_5&=\dfrac{1}{2}\left(\dfrac{11}{2}\right)+3=\dfrac{11}{4}+3=5.75 \\ \end{aligned}$
The sequence is strictly increasing. The sequence is bounded above by $6$.

$\displaystyle\lim_{n\to\infty}a_n=6$.
As shown in the remark, an explicit formula for this sequence is $a_n=6-\dfrac{1}{2^{n-3}}$.

\[\begin{aligned} a_1&=2,\qquad a_{n+1}=\dfrac{1}{2}a_n+3 \\ a_2&=\dfrac{1}{2}(2)+3=4 \\ a_3&=\dfrac{1}{2}(4)+3=5 \\ a_4&=\dfrac{1}{2}(5)+3=\dfrac{5}{2}+3=5.5 \\ a_5&=\dfrac{1}{2}\left(\dfrac{11}{2}\right)+3=\dfrac{11}{4}+3=5.75 \\ \end{aligned}\] The sequence appears to be increasing. It is not clear whether it is bounded.
We first assume the sequence has a limit and find the possible limits.
Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\displaystyle\lim_{n\to\infty}a_{n+1}=L$ also. Taking limits of both sides of the recursion relation gives \[\begin{aligned} &\lim_{n\to\infty} a_{n+1}=\lim_{n\to\infty} \dfrac{1}{2}a_n+3 \quad \Rightarrow \quad L=\dfrac{1}{2}L+3 \\ &\Rightarrow \quad 2L=L+6 \quad \Rightarrow \quad L=6 \end{aligned}\] So if the sequence has a limit, it must be $6$. Looking at the terms, we expect the limit is increasing to $6$.

We want to prove the sequence is increasing and bounded above by $6$ using mathematical induction. So we need to prove $a_n \lt a_{n+1} \lt 6$.
Initialization Step: $a_1 \lt a_2 \lt 6$ since $2 \lt 4 \lt 6$.
Induction Step: Assume $a_k \lt a_{k+1} \lt 6$ and prove $a_{k+1} \lt a_{k+2} \lt 6$. \[\begin{aligned} &a_k \lt a_{k+1} \lt 6 \quad \Rightarrow \quad \dfrac{1}{2}a_k \lt \dfrac{1}{2}a_{k+1} \lt 3 \\ &\Rightarrow \quad \dfrac{1}{2}a_k+3 \lt \dfrac{1}{2}a_{k+1}+3 \lt 6 \quad \Rightarrow \quad a_{k+1} \lt a_{k+2} \lt 6 \end{aligned}\] Hence the sequence is increasing from $2$ and bounded above by $6$. So by the Bounded, Monotonic Sequence Theorem the sequence converges to: \[ \lim_{n\to\infty} a_n=6 \]
ad

The limit of this sequence can also be found by first deriving an explicit formula for the terms. We know:
$a_1=2,\qquad a_{n+1}=\dfrac{1}{2}a_n+3$
$a_2=\dfrac{1}{2}(2)+3= 4$
$a_3=\dfrac{1}{2}(4)+3= 5$
$a_4=\dfrac{1}{2}(5)+3=\dfrac{11}{2}$
$a_5=\dfrac{1}{2}\left(\dfrac{11}{2}\right)+3=\dfrac{23}{4}$
$a_6=\dfrac{1}{2}\left(\dfrac{23}{4}\right)+3=\dfrac{47}{8}$

From the $4^\text{th}$ term on, each denominator is a power of $2$ and each numerator is $1$ less than $6$ times that denominator. e.g. \[a_5=\dfrac{6\cdot2^{5-3}-1}{2^{5-3}}\] so that in general we have \[a_n=\dfrac{6\cdot2^{n-3}-1}{2^{n-3}}\] which can be rewritten as: \[\begin{aligned} a_n=6-\dfrac{1}{2^{n-3}} \end{aligned}\]
Let us use mathematical induction to prove the formula:
1. $a_1=6-\dfrac{1}{2^{-2}}=6-4=2$
So the formula works for $n=1.$
2. Assume $a_k=6-\dfrac{1}{2^{k-3}}$ and prove that $a_{k+1}=6-\dfrac{1}{2^{k+1-3}}=6-\dfrac{1}{2^{k-2}}$.
Now: \[\begin{aligned} a_{k+1}&=\dfrac{1}{2}a_k+3 \\ &=\dfrac{1}{2}\left(6-\dfrac{1}{2^{k-3}}\right)+3 \\ &=3-\dfrac{1}{2\cdot2^{k-3}}+3 \\ &=6-\dfrac{1}{2^{k-2}} \end{aligned}\] which was to be shown. Hence the formula is correct for all $n$ by mathematical induction. With this formula, it is easy to find the limit: \[ \lim_{n\to\infty}a_n =\lim_{n\to\infty}\left(6-\dfrac{1}{2^{n-3}}\right)=6 \]
ad
$a_1=2,\qquad a_{n+1}=2a_n-3$

$\begin{aligned} a_1&=2,\qquad a_{n+1}=2a_n-3 \\ a_2&=1 \\ a_3&=-1 \\ a_4&=-5 \\ a_5&=-13 \\ \end{aligned}$
The sequence is decreasing for all $n$ and unbounded.
The sequence diverges to $-\infty$.

\[\begin{aligned} a_1&=2,\qquad a_{n+1}=2a_n-3 \\ a_2&=1 \\ a_3&=-1 \\ a_4&=-5 \\ a_5&=-13 \\ \end{aligned}\] It appears that the sequence is decreasing and may diverge to $-\infty$.
We first assume the sequence has a limit and find the possible limits.
Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\displaystyle\lim_{n\to\infty}a_{n+1}=L$ also. Taking limits of both sides of the recursion relation gives \[\begin{aligned} \lim_{n\to\infty} a_{n+1}=\lim_{n\to\infty} 2a_n-3 \quad &\Rightarrow \quad L=2L-3 \\ &\Rightarrow \quad L=3 \end{aligned}\] So if the sequence has a limit, it must be $3$ which is impossible if we can show the sequence is decreasing from $2$.

Let us use mathematical induction to show the sequence is decreasing. So we need to prove $a_n \gt a_{n+1}$.
Initialization Step: $a_1 \gt a_2$ since $2 \gt 1$.
Induction Step: Assume $a_k \gt a_{k+1}$ and prove $a_{k+1} \gt a_{k+2}$. \[\begin{aligned} a_k \gt a_{k+1} \quad &\Rightarrow \quad 2{a_k}^2-3 \gt 2{a_{k+1}}^2-3 \\ \quad &\Rightarrow \quad a_{k+1} \gt a_{k+2} \end{aligned}\] Hence the sequence is decreasing from $2$ and cannot have a limit of $3$. So by the Bounded, Monotonic Sequence Theorem the sequence is unbounded below and diverges to \[ \lim_{n\to\infty} a_n=-\infty \]
ad
$a_1=1,\qquad a_{n+1}=\dfrac{1}{3-a_n}$

$\begin{aligned} a_1&=1,\qquad a_{n+1}=\dfrac{1}{3-a_n} \\ a_2&=\dfrac{1}{2} \\ a_3&=\dfrac{1}{2.5}=.4 \\ a_4&=\dfrac{1}{2.6}=\dfrac{5}{13}=.385 \\ a_5&=\dfrac{1}{3-\dfrac{5}{13}}=\dfrac{13}{34}=.382 \\ \end{aligned}$
The sequence is strickly decreasing and bounded below by $0$.
$\lim\limits_{n\to\infty}a_n=\dfrac{3-\sqrt{5}}{2}\approx.382$

\[\begin{aligned} a_1&=1,\qquad a_{n+1}=\dfrac{1}{3-a_n} \\ a_2&=\dfrac{1}{2} \\ a_3&=\dfrac{1}{2.5}=.4 \\ a_4&=\dfrac{1}{2.6}=\dfrac{5}{13}=.385 \\ a_5&=\dfrac{1}{3-\dfrac{5}{13}}=\dfrac{13}{34}=.382 \\ \end{aligned}\] It appears that the sequence is decreasing and always positive.
We first assume the sequence has a limit and find the possible limits.
Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\displaystyle\lim_{n\to\infty}a_{n+1}=L$ also. Taking limits of both sides of the recursion relation gives \[\begin{aligned} &\lim_{n\to\infty} a_{n+1}=\lim_{n\to\infty} \dfrac{1}{3-a_n} \quad \Rightarrow \quad L=\dfrac{1}{3-L} \\ &\Rightarrow \quad L(3-L)=1 \quad \Rightarrow \quad L^2-3L+1=0 \\ &\Rightarrow \quad L=\dfrac{3\pm\sqrt{5}}{2}\approx2.62\,\text{or}\,.382 \end{aligned}\] So if the sequence has a limit, it must be $\dfrac{3+\sqrt{5}}{2}\approx2.62$ or $\dfrac{3-\sqrt{5}}{2}\approx.382$. Since the sequence starts at $1$, if we can show it's decreasing and bounded below, then the sequence must converge to $\dfrac{3-\sqrt{5}}{2}\approx.382$.

Let us use mathematical induction to show the sequence is decreasing and bounded below by $0$. So we will prove $1 \ge a_n \gt a_{n+1} \gt 0$. (We need the $1 \ge $ to be able to take reciprocals later.)
Initialization Step: $1 \ge a_1 \gt a_2 \gt 0$ since $1 \ge 1 \gt \dfrac{1}{2} \gt 0$.
Induction Step: Assume $1 \ge a_k \gt a_{k+1} \gt 0$ and prove $1 \ge a_{k+1} \gt a_{k+2} \gt 0$. \[\begin{aligned} 1 \ge a_k \gt a_{k+1} \gt 0 \quad &\Rightarrow \quad 2 \le 3-a_k \lt 3-a_{k+1} \lt 3 \\ &\Rightarrow \quad \dfrac{1}{2} \ge \dfrac{1}{3-a_k} \gt \dfrac{1}{3-a_{k+1}} \gt \dfrac{1}{3} \\ &\Rightarrow \quad 1 \ge \dfrac{1}{2} \ge a_{k+1} \gt a_{k+2} \gt \dfrac{1}{3} \gt 0 \end{aligned}\] Hence the sequence is decreasing from $1$ and bounded below by $0$. So by the Bounded, Monotonic Sequence Theorem the sequence converges to: \[ \lim_{n\to\infty} a_n=\dfrac{3-\sqrt{5}}{2}\approx.382 \]

ad
$a_1=2,\qquad a_{n+1}=\dfrac{4}{3+a_n}$

\[\begin{aligned} a_1&=2 &&a_{n+1}=\dfrac{1}{3+a_n} \\ a_2&=\dfrac{4}{3+2}&&=\dfrac{4}{5}=.80000 \\ a_3&=\dfrac{4}{3+\dfrac{4}{5}}&&=\dfrac{20}{19}=1.05263 \\ a_4&=\dfrac{4}{3+\dfrac{20}{19}}&&=\dfrac{76}{77}=.98701 \\ a_5&=\dfrac{4}{3+\dfrac{76}{77}}&&=\dfrac{308}{307}=1.00326 \\ a_6&=\dfrac{4}{3+\dfrac{308}{307}}&&=\dfrac{1228}{1229}=.99919 \\ \end{aligned}\] Here we have a non-monotonic sequence which seems to converge to $1$.
Notice that for odd indices, the terms appear to be decreasing, while for the even indices, they seem to be increasing. So try to show the odd numbered terms are decreasing and bounded below by $1$ while the even numbered terms are increasing and bounded above by $1$.

$\begin{aligned} a_1&=2 &&a_{n+1}=\dfrac{1}{3+a_n} \\ a_2&=\dfrac{4}{3+2}&&=\dfrac{4}{5}=.80000 \\ a_3&=\dfrac{4}{3+\dfrac{4}{5}}&&=\dfrac{20}{19}=1.05263 \\ a_4&=\dfrac{4}{3+\dfrac{20}{19}}&&=\dfrac{76}{77}=.98701 \\ a_5&=\dfrac{4}{3+\dfrac{76}{77}}&&=\dfrac{308}{307}=1.00326 \\ a_6&=\dfrac{4}{3+\dfrac{308}{307}}&&=\dfrac{1228}{1229}=.99919 \\ \end{aligned}$
The sequence is non-monotonic, but still converges to:
$\displaystyle \lim_{n\to\infty}a_n=1$

\[\begin{aligned} a_1&=2 &&a_{n+1}=\dfrac{1}{3+a_n} \\ a_2&=\dfrac{4}{3+2}&&=\dfrac{4}{5}=.80000 \\ a_3&=\dfrac{4}{3+\dfrac{4}{5}}&&=\dfrac{20}{19}=1.05263 \\ a_4&=\dfrac{4}{3+\dfrac{20}{19}}&&=\dfrac{76}{77}=.98701 \\ a_5&=\dfrac{4}{3+\dfrac{76}{77}}&&=\dfrac{308}{307}=1.00326 \\ a_6&=\dfrac{4}{3+\dfrac{308}{307}}&&=\dfrac{1228}{1229}=.99919 \\ \end{aligned}\] Here we have a non-monotonic sequence which seems to converge to $1$. Notice the odd numbered terms appear to be decreasing, while the even numbered terms appear to be increasing. We will show the odd terms and the even terms each approach $1$.

We first assume the limit exists and find the possible limits. Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\lim\limits_{n\to\infty}a_{n+1}=L$ also. Then the recursion formula says: \[\begin{aligned} \lim_{n\to\infty}a_{n+1}&=\lim_{n\to\infty}\dfrac{4}{3+a_n} \\ L&=\dfrac{4}{3+L} \\ L(3+L)&=4 \\ L^2+3L-4&=0 \\ (L-1)(L+4)&=0 \end{aligned}\] So if the limit exists, it must be either $L=1$ or $L=-4$. We expect $1$.

We first find the $2$ step recursion formula: \[ a_{n+2}=\dfrac{4}{3+a_{n+1}}=\dfrac{4}{3+\dfrac{4}{3+a_n}} \]

Let's begin with the odd numbered terms. To show these are decreasing and bounded below by $1$, we need to check $1 \lt a_{n+2} \lt a_n$.
For the initialization step, we have: $1 \lt a_3 \lt a_1$ since $1 \lt \dfrac{20}{19} \lt 2$ For the induction step we assume $1 \lt a_{k+2} \lt a_k$ and prove $1 \lt a_{k+4} \lt a_{k+2}$. So: \[\begin{aligned} &1 \lt a_{k+2} \lt a_k \\[4pt] \Rightarrow \quad &4 \lt 3+a_{k+2} \lt 3+a_k \\ \Rightarrow \quad &1 \gt \dfrac{4}{3+a_{k+2}} \gt \dfrac{4}{3+a_k} \\ \Rightarrow \quad &4 \gt 3+\dfrac{4}{3+a_{k+2}} \gt 3+\dfrac{4}{3+a_k} \\ \Rightarrow \quad &1 \lt \dfrac{4}{3+\dfrac{4}{3+a_{k+2}}} \lt \dfrac{4}{3+\dfrac{4}{3+a_k}} \\ \Rightarrow \quad &1 \lt a_{k+4} \lt a_{k+2} \end{aligned}\] So the limit of the odd sequence is $1$.

Now for the even terms. To show these are increasing and bounded above by $1$, we check $0 \lt a_n \lt a_{n+2} \lt 1$. (We need the $0 \lt$ so we can take reciprocals and know the inequalities reverse.)
For the initialization step, we have: $0 \lt a_2 \lt a_4 \lt 1$ since $0 \lt \dfrac{4}{5} \lt \dfrac{76}{77} \lt 1$ For the induction step we assume $0 \lt a_k \lt a_{k+2} \lt 1$ and prove $0 \lt a_{k+2} \lt a_{k+4} \lt 1$. So: \[\begin{aligned} &0 \lt a_k \lt a_{k+2} \lt 1 \\[4pt] \Rightarrow \quad &0 \lt 3+a_k \lt 3+a_{k+2} \lt 4 \\ \Rightarrow \quad &\dfrac{4}{3+a_k} \gt \dfrac{4}{3+a_{k+2}} \gt 1 \\ \Rightarrow \quad &3+\dfrac{4}{3+a_k} \gt 3+\dfrac{4}{3+a_{k+2}} \gt 4 \\ \Rightarrow \quad &0 \lt \dfrac{4}{3+\dfrac{4}{3+a_k}} \lt \dfrac{4}{3+\dfrac{4}{3+a_{k+2}}} \lt 1 \\ \Rightarrow \quad &0 \lt a_{k+2} \lt a_{k+4} \lt 1 \\ \end{aligned}\] So the limit of the even sequence is also $1$.

Since the limit of both subsequences is $1$, we conclude that the limit of this sequence is $1$.
ad

A patient receives $5\,\text{mg}$ of a certain drug daily. If in one $24$-hr day, the body eliminates $20\%$ of this drug, estimate the total amount that would be present after extended treatment.

Write a recursion relation for the amount of the drug present in the system just after a dose in terms of the amount a day before.

The maximum amount possible would be $25\,\text{mg}$.

On the first day there is $a_1=5\,\text{mg}$.
Each day there is $80\%$ of the drug from the previous day plus $5$ mg. So \[ a_{n+1}=0.8a_n+5 \] If there is a limit it must satisfy \[L=.8L+5 \implies L=25\,\text{mg}\] You can use mathematical induction to show the sequence is increasing and bounded above by $25$. So the limit is $25\,\text{mg}$.
ad

On the first day there is $a_1=5\,\text{mg}$.
Each day there is $80\%$ of the drug from the previous day plus $5$ mg. So \[ a_{n+1}=0.8a_n+5 \] If there is a limit it must satisfy \[L=.8L+5 \implies L=25\,\text{mg}\] To see if the sequence is increasing, we use mathematical induction.
1. $a_1=5$, $a_2=.8\cdot5+5=9$ So $a_1 \lt a_2$
2. Suppose $a_k \lt a_{k+1}$. Prove $a_{k+1} \lt a_{k+2}$:
$a_k \lt a_{k+1} \implies 0.8a_k \lt 0.8a_{k+1} \implies 0.8a_k+5 \lt 0.8a_{k+1}+5 \implies a_{k+1} \lt a_{k+2}$.
To check the sequence is bounded above by $25$, we use mathematical induction.
1. $a_1=5 \lt 25$
2. Suppose $a_k \lt 25$. Prove $a_{k+1} \lt 25$.
$a_k \lt 25 \implies 0.8a_k \lt 20 \implies 0.8a_k+5 \lt 25 \implies a_{k+1} \lt 25$.

ad
If $a_{n+1}=\dfrac{1}{2}a_n+3$, is there a value of $a_1$ for which the sequence does not converge? Does the limit of the sequence depend on the value of $a_1$?

Let $a_1=C$. Then try writing out the first $4$ terms and distributing the $\dfrac{1}{2}$ at each step. Generalize this to $a_n$. What happens as $n\to\infty$? Do you see a well-known infinite geometric series?

If that doesn't work, you can always fall back on induction proofs as done in the second solution.

The sequence converges for all values of $a_1$ and the limit is $6$ regardless of the value of $a_1$.

Consider the sequence defined by: \[ a_1=C \quad \text{and} \quad a_{n+1}=\dfrac{1}{2}a_n+3 \] Then \[\begin{aligned} a_2&=\dfrac{1}{2}C+3 \\ a_3&=\dfrac{1}{2}\left(\dfrac{1}{2}C+3.\right)+3=\dfrac{1}{ 2^2}C+\dfrac{3}{2}+3 \\ a_4&=\dfrac{1}{2^3}C+\dfrac{3}{2^2}+\dfrac{3}{2}+3 \\ &\qquad \vdots \\ a_n&=\dfrac{1}{2^{n-1}}C+\dfrac{3}{2^{n-2}}+\dfrac{3}{2^{n-3}}+...+\dfrac{3}{2}+3 \end{aligned}\] As $n\to\infty$, the first term $\to 0$ for any value of $C$. We write the others terms starting from the right and factoring out a $3$: \[ \lim_{n\to\infty} a_n =3\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...\dfrac{1}{2^{k-1}}+...\right) \] The quantity in parentheses is a well known infinite geometric series you first met in Algebra II and whose sum is $2$. Thus the limit of the sequence is \[ \lim_{n\to\infty} a_n=3(2)=6 \] for any the value of $C$.
ad

We re-solve the problem using the Bounded, Monotonic Sequence Theorem. Consider the sequence defined by: \[ a_1=C \quad \text{and} \quad a_{n+1}=\dfrac{1}{2}a_n+3 \] We first assume the sequence has a limit and find the possible limits.
Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\displaystyle\lim_{n\to\infty}a_{n+1}=L$ also. Taking limits of both sides of the recursion relation gives \[\begin{aligned} &\lim_{n\to\infty} a_{n+1}=\lim_{n\to\infty} \dfrac{1}{2}a_n+3 \quad \Rightarrow \quad L=\dfrac{1}{2}L+3 \\ &\Rightarrow \quad \dfrac{1}{2}L=3 \quad \Rightarrow \quad L=6 \end{aligned}\] So if the sequence has a limit, it must be $6$. So we look at three cases: $C=6$, $C \gt 6$ and $C \lt 6$.

Case 1: If $a_1=C=6$, then we claim $a_n=6$ for all $n$.
Initialization Step: $a_1=C=6$.
Induction Step: Assume $a_k=6$ and prove $a_{k+1}=6$. \[ a_{k+1}=\dfrac{1}{2}a_k+3=\dfrac{1}{2}6+3=6 \] So $\displaystyle \lim_{n\to\infty} a_n=6$ if $a_1=C=6$.

Case 2: If $a_1=C \gt 6$, then we claim $a_n$ is decreasing and bounded below by $6$. So we need to prove $a_n \gt a_{n+1} \gt 6$.
Initialization Step: Since $a_1 \gt 6$, we have $\dfrac{1}{2}a_1 \gt 3$. On one hand, we add $\dfrac{1}{2}a_1$ to both sides to get \[ a_1=\dfrac{1}{2}a_1+\dfrac{1}{2}a_1 \gt \dfrac{1}{2}a_1+3=a_2 \] On the other hand, we add $3$ to both sides to get \[ a_2=\dfrac{1}{2}a_1+3 \gt 6 \]
Induction Step: Assume $a_k \gt a_{k+1} \gt 6$ and prove $a_{k+1} \gt a_{k+2} \gt 6$. \[\begin{aligned} &a_k \gt a_{k+1} \gt 6 \quad \Rightarrow \quad \dfrac{1}{2}a_k \gt \dfrac{1}{2}a_{k+1} \gt 3 \\ &\Rightarrow \quad \dfrac{1}{2}a_k+3 \gt \dfrac{1}{2}a_{k+1}+3 \gt 6 \quad \Rightarrow \quad a_{k+1} \gt a_{k+2} \gt 6 \end{aligned}\] Hence the sequence is decreasing from $a_1=C$ and bounded below by $6$. So by the Bounded, Monotonic Sequence Theorem the sequence converges to \[ \lim_{n\to\infty} a_n=6 \]

Case 3: If $a_1=C \lt 6$, then we claim $a_n$ is increasing and bounded above by $6$. So we need to prove $a_n \lt a_{n+1} \lt 6$.
Initialization Step: Since $a_1 \lt 6$, we have $\dfrac{1}{2}a_1 \lt 3$. On one hand, we add $\dfrac{1}{2}a_1$ to both sides to get \[ a_1=\dfrac{1}{2}a_1+\dfrac{1}{2}a_1 \lt \dfrac{1}{2}a_1+3=a_2 \] On the other hand, we add $3$ to both sides to get \[ a_2=\dfrac{1}{2}a_1+3 \lt 6 \]
Induction Step: Assume $a_k \lt a_{k+1} \lt 6$ and prove $a_{k+1} \lt a_{k+2} \lt 6$. \[\begin{aligned} &a_k \lt a_{k+1} \lt 6 \quad \Rightarrow \quad \dfrac{1}{2}a_k \lt \dfrac{1}{2}a_{k+1} \lt 3 \\ &\Rightarrow \quad \dfrac{1}{2}a_k+3 \lt \dfrac{1}{2}a_{k+1}+3 \lt 6 \quad \Rightarrow \quad a_{k+1} \lt a_{k+2} \lt 6 \end{aligned}\] Hence the sequence is increasing from $a_1=C$ and bounded above by $6$. So by the Bounded, Monotonic Sequence Theorem the sequence converges to \[ \lim_{n\to\infty} a_n=6 \]

Thus, the sequence converges for all values of $a_1$ and $\displaystyle \lim_{n\to\infty} a_n=6$ regardless of the value of $a_1$.

ad
If $a_{n+1}=2a_n-3$, is there a value of $a_1$ for which the sequence converges? Is there a second value?

The only value for $a_1$ when $a_{n+1}=2a_n-3$ converges is $a_1=3$.

Consider the sequence defined by: \[ a_1=C \quad \text{and} \quad a_{n+1}=2a_n-3 \] We first assume the sequence has a limit and find the possible limits.
Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\displaystyle\lim_{n\to\infty}a_{n+1}=L$ also. Taking limits of both sides of the recursion relation gives \[\begin{aligned} &\lim_{n\to\infty} a_{n+1}=\lim_{n\to\infty} 2a_n-3 \\ &\Rightarrow \quad L=2L-3 \quad \Rightarrow \quad L=3 \end{aligned}\] So if the sequence has a limit, it must be $3$. So we look at three cases: $C=3$, $C \gt 3$ and $C \lt 3$.

Case 1: If $a_1=C=3$, then we claim $a_n=3$ for all $n$.
Initialization Step: $a_1=C=3$.
Induction Step: Assume $a_k=3$ and prove $a_{k+1}=3$. \[ a_{k+1}=2a_k-3=2\cdot3-3=3 \] So $\displaystyle \lim_{n\to\infty} a_n=3$ if $a_1=C=3$.

Case 2: We want to know what happens if $a_1=C \gt 3$. For example, if $a_1=4$ then $a_2=2\cdot4-3=5$ and the sequence increases. Maybe it always increases. So suppose $a_1=C \gt 3$. If we can show $a_n$ is increasing, since there cannot be any limit other than $3$, the sequence must be unbounded. So we want to show $a_n \lt a_{n+1}$.
Initialization Step: Since $a_1 \gt 3$, we have $a_1-3 \gt 0$. Adding $a_1$ to both sides gives: \[ a_2=2a_1-3 \gt a_1 \]
Induction Step: Assume $a_k \lt a_{k+1}$ and prove $a_{k+1} \lt a_{k+2}$. \[\begin{aligned} &a_k \lt a_{k+1} \quad \Rightarrow \quad 2a_k \lt 2a_{k+1} \\ &\Rightarrow \quad 2a_k-3 \lt 2a_{k+1}-3 \quad \Rightarrow \quad a_{k+1} \lt a_{k+2} \end{aligned}\] Hence the sequence is increasing from $a_1=C \gt 3$ and unbounded. So by the Bounded, Monotonic Sequence Theorem the sequence converges to \[ \lim_{n\to\infty} a_n=\infty \]

Case 3: We want to know what happens if $a_1=C \lt 3$. For example, if $a_1=2$ then $a_2=2\cdot2-3=1$ and the sequence decreases. Maybe it always decreases. So suppose $a_1=C \lt 3$. If we can show $a_n$ is decreasing, since there cannot be any limit other than $3$, the sequence must be unbounded. So we want to show $a_n \gt a_{n+1}$.
Initialization Step: Since $a_1 \lt 3$, we have $a_1-3 \lt 0$. Adding $a_1$ to both sides gives: \[ a_2=2a_1-3 \lt a_1 \]
Induction Step: Assume $a_k \gt a_{k+1}$ and prove $a_{k+1} \gt a_{k+2}$. \[\begin{aligned} &a_k \gt a_{k+1} \quad \Rightarrow \quad 2a_k \gt 2a_{k+1} \\ &\Rightarrow \quad 2a_k-3 \gt 2a_{k+1}-3 \quad \Rightarrow \quad a_{k+1} \gt a_{k+2} \end{aligned}\] Hence the sequence is decreasing from $a_1=C \lt 3$ and unbounded. So by the Bounded, Monotonic Sequence Theorem the sequence converges to \[ \lim_{n\to\infty} a_n=-\infty \]

Thus, the sequence converges to $\displaystyle \lim_{n\to\infty} a_n=3$ if $a_1=3$, diverges to $\displaystyle \lim_{n\to\infty} a_n=\infty$ if $a_1 \gt 3$ and diverges to $\displaystyle \lim_{n\to\infty} a_n=-\infty$ if $a_1 \lt 3$.

So $a_1=3$ is the only value of $a_1$ for which the sequence converges.

ad

e. Precise Definitions and Proofs

Prove the Subtraction Law directly, without using the Addition Law.

Let $a_n$ and $b_n$ be sequences for which $\displaystyle \lim_{n\to\infty}a_n=L$ and $\displaystyle \lim_{n\to\infty}b_n=M$ where $L$ and $M$ are finite. Then: \[ \lim_{n\to\infty}(a_n-b_n)=L-M \]

The conditions $\displaystyle \lim_{n\to\infty}a_n=L$ and $\displaystyle \lim_{n\to\infty}b_n=M$ say: For all $\varepsilon_1 \gt 0$, there is a positive integer, $N_1$, such that if $n \gt N_1$ then $|a_n-L| \lt \varepsilon_1$.
For all $\varepsilon_2 \gt 0$, there is a positive integer, $N_2$, such that if $n \gt N_2$ then $|b_n-M| \lt \varepsilon_2$. We need to show $\displaystyle \lim_{n\to\infty}(a_n-b_n)=L-M$ which means: For all $\varepsilon \gt 0$, there is a positive integer, $N$, such that if $n \gt N$ then $|a_n-b_n-L+M| \lt \varepsilon$. So given an arbitrary number $\varepsilon \gt 0$, we let \[ \varepsilon_1=\varepsilon_2=\dfrac{\varepsilon}{2} \] and pick $N_1$ and $N_2$ to satisfy the definitions of the limits of $a_n$ and $b_n$. Then, let $N=\max(N_1,N_2)$. Then, if $n \gt N$ then $n \gt N_1$ and $n \gt N_2$. Consequently, \[ |a_n-L| \lt \varepsilon_1=\dfrac{\varepsilon}{2} \quad \text{and} \quad |b_n-M| \lt \varepsilon_2=\dfrac{\varepsilon}{2} \] Finally, by the Triangle Inequality: \[\begin{aligned} |a_n-b_n-L+M|&=|(a_n-L)-(b_n-M)| \\ &\le |a_n-L|+|-(b_n-M)| \\ =|a_n-L|&+|b_n-M| \lt \dfrac{\varepsilon}{2}+\dfrac{\varepsilon}{2}=\varepsilon \end{aligned}\]
Prove: If a sequence is unbounded, then it cannot have a limit.

We use proof by contradiction. Assume the sequence, $a_n$, is unbounded but does have a limit, i.e. $\lim\limits_{n\to\infty}a_n=L$. This means: For all $\varepsilon \gt 0$, there is a positive integer, $N$, such that if $n \gt N$ then $|a_n-L| \lt \varepsilon$. Pick $\varepsilon=1$. Then, there is a positive number $N$ such that for every $n \gt N$, we have $|a_n-L|\lt 1$. This means $L-1\lt a_n\lt L+1$ for all $n \gt N$. In other words, all but finitely many terms of the sequence are bounded between $L-1$ and $L+1$. If we let $m=\min(a_1,a_2,\ldots,a_N,L-1)$ and $M=\max(a_1,a_2,\ldots,a_N,L+1)$ then $m \le a_n \le M$ for all $n$ and the sequence is bounded. This contradicts the hypothesis that the sequence is unbounded. Consequently, the sequence cannot have a limit.
Give Examples: If a sequence is not monotonic, it may or may not have a limit.

In two previous problems we saw examples of non-monotonic sequences that converge. \[ \dfrac{n+\sin\left(\dfrac{n\pi}{2}\right)}{n}\to 1 \quad \text{and} \quad \dfrac{-2n+\sin\left(\dfrac{n\pi}{2}\right)}{n}\to-2 \] On the other hand, the sequences $c_n=2+(-1)^n$ and $a_n=\sin\dfrac{n\pi}{2}$ are divergent non-monotonic sequences.

Review Exercises

Write the first five terms of each sequence and determine the limit if convergent.

$a_n=\dfrac{6}{(n+1)(n^2-n+6)}$

$ a_1=\dfrac{1}{2} \quad a_2=\dfrac{1}{4} \quad a_3=\dfrac{1}{8} \quad a_4=\dfrac{1}{15} \quad a_5=\dfrac{1}{26} $
$\displaystyle \lim\limits_{n\to\infty}a_n=0$

\[ a_1=\dfrac{1}{2} \qquad a_2=\dfrac{1}{4} \qquad a_3=\dfrac{1}{8} \qquad a_4=\dfrac{1}{15} \qquad a_5=\dfrac{1}{26} \] It appears the limit is $0$. We compute: \[\begin{aligned} \lim_{n\to\infty}\dfrac{6}{(n+1)(n^2-n+6)}&= \dfrac{6}{\lim\limits_{n\to\infty}((n+1)(n^2-n+6))} \\ &=\dfrac{6}{\infty}=0 \end{aligned}\]

ad
$a_n=\dfrac{n(n+1)(n-4)}{6(n^2+3n-2)}$

$ a_1=-\dfrac{1}{2} \quad a_2=-\dfrac{1}{4} \quad a_3=-\dfrac{1}{8} \quad a_4=0 \quad a_5=\dfrac{5}{38} $
$\displaystyle \lim\limits_{n\to\infty}a_n=\infty$

\[ a_1=-\dfrac{1}{2} \qquad a_2=-\dfrac{1}{4} \qquad a_3=-\dfrac{1}{8} \qquad a_4=0 \qquad a_5=\dfrac{5}{38} \] The limit is not very clear, so we compute. We divide the numerator and denominator by $n^2$. \[\begin{aligned} \lim_{n\to\infty}\dfrac{n(n+1)(n-4)}{6(n^2+3n-2)} &=\lim_{n\to\infty}\dfrac{(n+1)\left(1-\dfrac{4}{n^2}\right)} {6\left(1+\dfrac{2}{n}-\dfrac{2}{n^2}\right)} \\ &=\infty \end{aligned}\]

ad

Determine whether each sequence converges or diverges. If convergent, find the limit. If divergent, does it approach $\infty$ or $-\infty$?

$n^{1/n}$

$\displaystyle \lim_{n\to\infty}n^{1/n}=1$

$n^{1/n}$ is of the form $\infty^0$, so we apply $e^{\ln}$ inside the limit, pull the exponential out of the limit, and pull the exponent $\dfrac{1}{n}$ out of the log: \[ \lim_{n\to\infty}n^{1/n} =\lim\limits_{n\to\infty}{\large e}^{\ln(n^{1/n})} =\large e^{\lim\limits_{n\to\infty} \frac{\ln(n)}{n}} \] Now $\lim\limits_{n\to\infty} \frac{\ln(n)}{n}$ is of the form $\dfrac{0}{0}$. So we apply l'Hospital's rule: \[ \lim_{n\to\infty}{\dfrac{\ln(n)}{n}} \overset{\text{l'H}}=\lim_{n\to\infty}{\dfrac{1}{n}}=0 \] Therefore \[ \lim_{n\to\infty}n^{1/n} =\large e^{\lim\limits_{n\to\infty} \frac{\ln(n)}{n}} =e^0=1 \]
ad
$\dfrac{\sin^2n}{2^n}$

$\displaystyle \lim_{n\to\infty}\dfrac{\sin^2n}{2^n}=0$

To compute this limit, we use the Sandwich Theorem. We know: \[ 0\le\sin^2n\le1 \] Then: \[\begin{aligned} &0\le\dfrac{\sin^2n}{2^n}\le2^{-n} \\ &0\le\lim_{n\to\infty}\dfrac{\sin^2n}{2^n}\le\lim_{n\to\infty}2^{-n} \\ &0\le\lim_{n\to\infty}\dfrac{\sin^2n}{2^n}\le0 \\ \end{aligned}\] Therefore: \[ \lim_{n\to\infty}\dfrac{\sin^2n}{2^n}=0 \]
ad
$\dfrac{(n+1)!}{3\cdot n!}$

$\displaystyle\lim_{n\to\infty}\dfrac{(n+1)!}{3\cdot n!}=\infty$

Since $(n+1)!=(n+1)\cdot n!$, we have: \[\lim_{n\to\infty}\dfrac{(n+1)!}{3\cdot n!} =\lim_{n\to\infty}\dfrac{n+1}{3}=\infty\]
ad
$\left(1-\dfrac{1}{n}\right)^n$

$\displaystyle\lim_{n\to\infty}\left(1-\dfrac{1}{n}\right)^n=e^{-1}$

We insert an $e^{\ln}$ into the limit, move the limit inside the exponential and move the exponent $n$ out of the log: \[ \lim_{n\to\infty}\left(1-\dfrac{1}{n}\right)^n= \lim_{n\to\infty}{\large e}^{\scriptstyle \ln\left(1-\frac{\scriptstyle 1}{\scriptstyle n}\right)^n} ={\large e}^{\scriptstyle \lim\limits_{n\to\infty}n\ln\left(1-\frac{\scriptstyle 1}{\scriptstyle n}\right)} \] Now $\displaystyle \lim_{n\to\infty}n\ln\left(1-\dfrac{1}{n}\right)$ is of the form $\infty\cdot0$, so we write it as $\displaystyle\lim_{n\to\infty}\dfrac{\ln\left(1-\dfrac{1}{n}\right)}{\dfrac{1}{n}}$ which has the form $\dfrac{0}{0}$ and then we can use l'Hospital's Rule: \[\begin{aligned} \lim_{n\to\infty} n\ln\left(1-\dfrac{1}{n}\right) &=\lim_{n\to\infty}\dfrac{\ln\left(1-\dfrac{1}{n}\right)}{\dfrac{1}{n}} =\lim_{n\to\infty}\dfrac{\dfrac{1}{1-\dfrac{1}{n}}n^{-2}}{-n^{-2}} \\ &=\lim_{n\to\infty}\dfrac{1}{1-\dfrac{1}{n}}(-1)=-1 \end{aligned}\] Therefore: \[ \lim_{n\to\infty}\left(1-\dfrac{1}{n}\right)^n=e^{-1} \]
ad
$ne^{-n/2}$

$\displaystyle \lim_{n\to\infty} ne^{-n/2}=0$

The limit has form $\infty\cdot0$, so we write the $e^{-n/2}$ factor as $e^{n/2}$ in the denominator: \[ \lim_{n\to\infty}ne^{-n/2}=\lim_{n\to\infty}\dfrac{n}{e^{n/2}} \] Now the limit has form $\dfrac{\infty}{\infty}$, so we apply l'Hospital's rule: \[ \lim_{n\to\infty}\dfrac{n}{e^{n/2}} \overset{\text{l'H}}=\lim_{n\to\infty}\dfrac{1}{\dfrac{1}{2}e^{n/2}}=0 \]
ad
$\sqrt[\scriptstyle n]{n^2+5}$

$\displaystyle \lim_{n\to\infty}\sqrt[\scriptstyle n]{n^2+5}=1$

We first rewrite the expression as $(n^2+5)^{1/n}$, and observe the sequence is of the form $\infty^0$, so we apply $e^{\ln}$ inside the limit, move the limit inside the exponential, and move the exponent $\dfrac{1}{n}$ outside the log: \[\begin{aligned} \lim_{n\to\infty}(n^2+5)^{1/n} &=\lim_{n\to\infty}{\large e}^{\ln(n^2+5)^{1/n}} \\ &={\large e}^{\small \lim\limits_{n\to\infty} \frac{\ln(n^2+5)}{n}} \end{aligned}\] Now $\displaystyle \lim_{n\to\infty} \dfrac{\ln(n^2+5)}{n}$ has the form $\dfrac{\infty}{\infty}$. So we apply l'Hospital's rule: \[ \lim_{n\to\infty} \dfrac{\ln(n^2+5)}{n} \overset{\text{l'H}}=\lim_{n\to\infty}\dfrac{2n}{n^2+5} \] But $\lim\limits_{n\to\infty}\dfrac{2n}{n^2+5}$ is still of the form $\dfrac{\infty}{\infty}$! So we have to apply l'Hospital's rule again. \[ \lim_{n\to\infty}\dfrac{2n}{n^2+5} \overset{\text{l'H}}=\lim_{n\to\infty}\dfrac{2}{2n} =0 \] Therefore: \[ \lim_{n\to\infty}\sqrt[\scriptstyle n]{n^2+5}=e^0=1 \]
ad

Determine whether each recursively defined sequence is monotonic, bounded, convergent or divergent. If convergent find the limit.

$a_1=\dfrac{1}{2} \qquad a_{n+1}=\dfrac{1}{1-a_n}$

Write out the first $4$ terms of the sequence.

The sequence is oscillatory divergent and not monotonic, but it is bounded above by $2$ and bounded below by $-1$.

Notice: \[ a_1=\dfrac{1}{2} \qquad a_2=2 \qquad a_3=-1 \qquad a_4=\dfrac{1}{2} \] $\begin{aligned} a_1&=\dfrac{1}{2} \\ a_2&=2 \\ a_3&=-1 \\ a_4&=\dfrac{1}{2} \end{aligned}$
Since $a_4=a_1$, the sequence will cycle between $\dfrac{1}{2},2,-1$ and cannot have a limit. So the sequence is oscillatory divergent and not monotonic, but it is bounded above by $2$ and bounded below by $-1$.
ad
$a_1=1 \qquad a_{n+1}=2\sqrt{a_n+3}$

The sequence is increasing and bounded above by 6.
$\displaystyle \lim_{n\to\infty}a_n=6$

\[\begin{aligned} a_1&=1,\qquad a_{n+1}=2\sqrt{a_n+3} \\ a_2&=2\sqrt{4}=4 \\ a_3&=2\sqrt{7}\approx5.29 \\ a_4&=2\sqrt{2\sqrt{7}+3}\approx5.76 \end{aligned}\] The sequence appears to be increasing. It is not clear whether it is bounded.
We first assume the sequence has a limit and find the possible limits.
Let $\displaystyle L=\lim_{n\to\infty}a_n$. Then $\displaystyle\lim_{n\to\infty}a_{n+1}=L$ also. Taking limits of both sides of the recursion relation gives \[\begin{aligned} &\lim_{n\to\infty} a_{n+1}=\lim_{n\to\infty} 2\sqrt{a_n+3} \quad \Rightarrow \quad L=2\sqrt{L+3} \\ &\Rightarrow \quad L^2=4(L+3) \quad \Rightarrow \quad L^2-4L-12=0 \\ &\Rightarrow \quad (L+2)(L-6)=0 \quad \Rightarrow \quad L=-2,6 \end{aligned}\] So if the sequence has a limit, it must be either $-2$ or $6$. Looking at the terms, we expect the limit is increasing to $6$.

We want to prove the sequence is increasing and bounded above by $6$ using mathematical induction. So we need to prove $a_n \lt a_{n+1} \lt 6$.
Initialization Step: $a_1 \lt a_2 \lt 6$ since $1 \lt 4 \lt 6$.
Induction Step: Assume $a_k \lt a_{k+1} \lt 6$ and prove $a_{k+1} \lt a_{k+2} \lt 6$. \[\begin{aligned} &a_k \lt a_{k+1} \lt 6 \quad \Rightarrow \quad a_k+3 \lt a_{k+1}+3 \lt 9 \\ &\Rightarrow \quad \sqrt{a_k+3} \lt \sqrt{a_{k+1}+3} \lt 3 \\ &\Rightarrow \quad 2\sqrt{a_k+3} \lt 2\sqrt{a_{k+1}+3} \lt 6 \\ &\Rightarrow \quad a_{k+1} \lt a_{k+2} \lt 6 \end{aligned}\] Hence the sequence is increasing from $1$ and bounded above by $6$. So by the Bounded, Monotonic Sequence Theorem the sequence converges to: \[ \lim_{n\to\infty} a_n=6 \]
ad

A government project now costing $$3$ million a year is to be reduced by $2\%$ per year beginning in $2000$.
1. Write an expression for the amount budgeted for the program after $n$ years.
  
  $a_n=3\,000\,000(.98)^n$
  
  Each year the amount budgeted will be the amount budgeted the year before times $.98$ (since the amount budgeted is reduced by $2\%$ a year and $1-.02=.98$). The original amount budgeted was $$3\,000\,000$. So the amount budgeted after $n$ years is: \[ a_n=\text{\$}3\,000\,000(.98)^n \]
  ad
2. How long will it take for the program cost to be reduced by $1$ million?
  
  $n=\log_{.98}\left(\dfrac{2}{3}\right)\approx20.07\approx20\,\text{years}$
  
  From part (a) we found the amount budgeted after $n$ years is $a_n=3\,000\,000(.98)^n$. We solve for $n$ when the amount budgeted is equal to $2$ million (since $3$ million minus $1$ million is equal to $2$ million): \[\begin{aligned} 3\,000\,000(.98)^n&=2\,000\,000 \\ (.98)^n&=\dfrac{2}{3} \\ n&=\log_{.98}\left(\dfrac{2}{3}\right)\approx20.07\,\text{years} \end{aligned}\]
  ad
3. Does the sequence of budgeted amounts converge?
  
  The sequence converges to $\displaystyle \lim_{n\to\infty} a_n=0$
  
  From part (a) we found the amount budgeted after $n$ years is $a_n=3\,000\,000(.98)^n$.
  We take the limit of this: \[ \lim_{n\to\infty} a_n=\lim_{n\to\infty} 3\,000\,000(.98)^n=0 \] since $.98 \lt 1$.
  ad

PY: All Checked to here
Except for precise proofs of Reciprocal, Quotient and Power Laws

PY: Move these to after 26.

$\displaystyle \lim_{n\to\infty} \left(\sqrt{n^2+5n}-\sqrt{n^2-3n}\right)$

Multiply and divide by the conjugate.

$\displaystyle \lim_{n\to\infty} \left(\sqrt{n^2+5n}-\sqrt{n^2-3n}\right)=4$

xxx
$\displaystyle \lim_{n\to\infty} \left(n-\sqrt{n+2}\sqrt{n+8}\right)$

Multiply and divide by the conjugate.

$\displaystyle \lim_{n\to\infty} \left(n-\sqrt{n+2}\sqrt{n+8}\right)=-5$

xxx
$\displaystyle \lim_{n\to\infty} \left(\ln(12n^2+n)-\ln(4n^2-3n)\right)$

Combine the logs.

$\displaystyle \lim_{n\to\infty} \left(\ln(12n^2+n)-\ln(4n^2-3n)\right)=\ln3$

xxx
$\displaystyle \lim_{n\to\infty} \left(\dfrac{n+5}{n}\right)^n$

Apply $e^{\ln}$ to the limit.

$\displaystyle \lim_{n\to\infty} \left(\dfrac{n+5}{n}\right)^n=e^5$

xxx
$\displaystyle \lim_{n\to\infty} \left(\dfrac{n+5}{n+2}\right)^{2n}$

Apply $e^{\ln}$ to the limit.

$\displaystyle \lim_{n\to\infty} \left(\dfrac{n+5}{n+2}\right)^{2n}=e^6$

xxx
$\displaystyle \lim_{n\to\infty} \left(\dfrac{1}{\ln n}\right)^{\ln n}$

Apply $e^{\ln}$ to the limit.

$\displaystyle \lim_{n\to\infty} \left(\dfrac{1}{\ln n}\right)^{\ln n}=0$

xxx
$\displaystyle \lim_{n\to\infty} \left(\dfrac{1}{\ln n}\right)^{1/\ln n}$

Apply $e^{\ln}$ to the limit.

$\displaystyle \lim_{n\to\infty} \left(\dfrac{1}{\ln n}\right)^{1/\ln n}=1$

xxx
$\displaystyle \lim_{n\to\infty} \left(\dfrac{1}{\ln n}\right)^{n/\ln n}$

Apply $e^{\ln}$ to the limit.

$\displaystyle \lim_{n\to\infty} \left(\dfrac{1}{\ln n}\right)^{n/\ln n}=0$

xxx
$\displaystyle \lim_{n\to\infty} \left(\dfrac{1}{\ln n}\right)^{1/\ln(\ln n)}$

Apply $e^{\ln}$ to the limit.

$\displaystyle \lim_{n\to\infty} \left(\dfrac{1}{\ln n}\right)^{1/\ln(\ln n)}=\dfrac{1}{e}$

xxx